Witness (mathematics)

In mathematical logic, a witness is a specific value t to be substituted for variable x of an existential statement of the form ∃x φ(x) such that φ(t) is true.

Examples

For example, a theory T of arithmetic is said to be inconsistent if there exists a proof in T of the formula "0=1". The formula I(T), which says that T is inconsistent, is thus an existential formula. A witness for the inconsistency of T is a particular proof of "0 = 1" in T.

Boolos, Burgess, and Jeffrey (2002:81) define the notion of a witness with the example, in which S is an n-place relation on natural numbers, R is an n-place recursive relation, and ↔ indicates logical equivalence (if and only if):

" S(x₁, ..., x_n) ↔ ∃y R(x₁, . . ., x_n, y)

" A y such that R holds of the x_i may be called a 'witness' to the relation S holding of the x_i (provided we understand that when the witness is a number rather than a person, a witness only testifies to what is true)." In this particular example, B-B-J have defined s to be (positively) recursively semidecidable, or simply semirecursive.

Henkin witnesses

In predicate calculus, a Henkin witness for a sentence 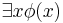in a theory T is a term c such that T proves φ(c) (Hinman 2005:196). The use of such witnesses is a key technique in the proof of Gödel's completeness theorem presented by Leon Henkin in 1949.

References

• George S. Boolos, John P. Burgess, and Richard C. Jeffrey, 2002, Computability and Logic: Fourth Edition, Cambridge University Press, ISBN 0-521-00758-5.
• Leon Henkin, 1949, "The completeness of the first-order functional calculus", Journal of Symbolic Logic v. 14 n. 3, pp. 159–166.
• Peter G. Hinman, 2005, Fundamentals of mathematical logic, A.K. Peters, ISBN 1-568-81262-0,